اعداد اعجاب انگیز فیبوناچی در تحلیل تکنیکال
فهرست مطالب مقاله اعداد اعجاب انگیز فیبوناچی
در ریاضیات سری اعداد مهم فیبوناچی به دنبالهای از اعداد گفته میشود که به صورت زیر تعریف میشود:
Fn=F(n-1) + F(n+1) ; n=0 –> Fn=0;n=1–> Fn=1
غیر از دو عدد اول اعداد بعدی از جمع دو عدد قبلی خود بدست میآید. اولین جملات سری اعداد فیبوناچی عبارتاند از:
۰,۱,۱,۲,۳,۵,۸,۱۳,۲۱,۳۴,۵۵,۸۹,۱۴۴,۲۳۳,۳۷۷,۶۱۰,۹۸۷,۱۵۹۷,۲۵۸۴,۴۱۸۱,۶۷۶۵,۱۰۹۴۶,۱۷۷۱۱
این اعداد به نام لئوناردو فیبوناچی ریاضیدان ایتالیایی نامگذاری شدهاست. وی نخستین ریاضیدان بزرگ اروپا در قرن سیزدهم است که بیشتر فعالیت هایش از آثار ریاضیدان های مسلمان به خصوص خوارزمی، کرجی و ابوکامل تأثیر پذیرفته است.
در این مقاله به بررسی اعداد فیبوناچی، نسبت طلایی و اعداد مهم فیبوناچی می پردازیم.
فیبوناچی در تحلیل تکنیکال
فیبوناچی در تحلیل تکنیکال می تواند تاثیرات مختلفی داشت باشد. دیگر همه فعالان بورس و بازار های ارزی، با مباحث مربوط به تحلیل تکنیکال آشنا هستند. این تحلیل ها می توانند تاثیرات مختلفی را بر روی فعالیت های اصلی افراد داشته باشند. اگر شما هم قصد استفاده از فیبوناچی در تحلیل تکنیکال را دارید، در ادامه با ما همراه باشید.
فیبوناچی چیست؟
فیبوناچی به دنباله قوی از اعداد گفته می شود که ترکیب خاصی دارد. در این ترکیب، شمارش از 1 شروع شده و ادامه پیدا می کند. بر خلاف 2 عدد اول، همه اعداد، از جمع دو عدد قبلی به دست می آیند. یعنی ترکیب به صورت زیر ایجاد می شود.
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 …
مسلما این دنبال عددی می تواند تاثیرات مختلفی را در بازار های بورسی داشته باشد. به همین علت هم فعالان این بازار باید با مباحث مقدماتی مربوط به این دنباله آشنا باشند.
کاربرد این رشته اعداد در تحلیل تکنیکال
فیبوناچی در تحلیل تکنیکال، سطوح مختلفی دارد. این سطوح می توانند مجموعه خطوط افقی باشند که حمایت و مقاومت را به ما نشان می دهند. هر سطح در فیبوناچی یک درصد خاص دارد که این درصد از اهمیت بالایی برخوردار است.
فیبوناچی در تحلیل تکنیکال، یک ابزار جادویی به حساب نمی آید. شما نمی توانید با استفاده از این ابزار به صورت قطعی نتیجه نهایی را بررسی کنید. ولی، این ابزار ها می توانند برای عدم قطعیت کاربرد داشته باشند. خیلی از متخصصان معتقد هستند که از دنباله فیبوناچی نمی توان به عنوان یک ابزار برای معامله استفاده کرد. ولی در کل دنباله فیبوناچی یک دنباله به شدت مهم و کاربردی در تحلیل های تکنیکال بوده که اهمیت فوق العاده بالایی دارد. معمولا فیبوناچی می تواند سطوح حمایت و مقاومت تقلبی را ایجاد کند. در نتیجه، شما باید به این مسئله هم توجه ویژه ای داشته باشید.
پیشنهاد تی بورس : آموزش فارکس در مشهد
نسبت طلایی اعداد فیبوناچی
دنباله اعداد فیبوناچی را بار دیگر در نظر می گیریم:
- ۱۰—-۹—-۸—-۷—-۶—-۵—-۴—-۳—-۲—-۱—-شماره جمله
- ۵۵—-۳۴—-۲۱—-۱۳—-۸—-۵—-۳—-۲—-۱—-۱—-مقدار جمله
- نسبت جمله دوم به اول برابر است با ۱
- نسبت جمله سوم به دوم برابر است با ۲
- نسبت جمله چهارم به سوم برابر است با ۱٫۵
- نسبت جمله پنجم به چهارم برابر است با ۱٫۶۶
- نسبت جمله ششم به پنجم برابر است با ۱٫۶
- نسبت جمله هفتم به ششم برابر است با ۱٫۶۲۵
- نسبت جمله هشتم به هفتم برابر است با ۱٫۶۱۵
- نسبت جمله نهم به هشتم برابر است با ۱٫۶۱۹
- نسبت جمله دهم به نهم برابر است با ۱٫۶۱۷
به نظر میرسد که این رشته به عدد طلایی نزدیک میشود. اگر نسبت عدد چهلم این رشته را به عدد قبلی حساب کنیم به عدد ۱٫۶۱۸۰۳۳۹۸۸۷۴۹۸۹۵ میرسیم که با تقریب ۱۴ رقم اعشار نسبت طلایی را نشان میدهد. نسبت جملات متوالی به عدد طلایی میل میکند.
در توالی اعداد فیبوناچی، در صورت در نظر نگرفتن چند جمله اول این دنباله، مابقی اعداد تقریبا 1.618 برابر عدد ما قبل خود است.
زاویه φ
معادله خطی به صورت y=mx در نظر میگیریم m .به معنی شیب خط است و یک عدد حقیقی است. میدانیم اگر m گنگ باشد، خط y=mx از هیچ نقطهای با مختصات صحیح به جز مبدأ عبور نخواهد کرد. در واقع این خط امکان ندارد از نقطهای (جز مبدأ) عبور کند که هم x و هم y آن عدد صحیح باشند.
حال به جای m قرار میدهیم: φ. یعنی خط y=φx را در نظر میگیریم. چون φ هم یک عدد گنگ است، این خط از هیچ نقطهای با x و yy صحیح (جز مبدأ) عبور نخواهد کرد. به همین دلیل نقطههایی را با x و y صحیح در نظر میگیریم که کمترین فاصله را از این خط دارند. ابتدا به نظر میرسد نقطه (۱,۱) کمترین فاصله را با این خط دارد. ولی فاصله نقطه (۱,۲) از این خط کمتر است.
نقطه (۳,۲۲) فاصله کمتری با این خط دارد. همچنین فاصله نقطه (۳,۵) از این هم کمتر است. این نقاط به همین ترتیب ادامه خواهند یافت و در زیر چند نقطه بعدی را که فاصلهشان از این خط کمتر میشود را میبینید:
… ، (۳۴,۵۵)، (۲۱,۳۴)، (۱۳,۲۱)، (۸,۱۳)، (۵,۸)، (۳,۵)، (۲,۳)، (۱,۲)، (۱,۱)
صحت مطالب فوق به راحتی قابل بررسی است. با کمی دقت در مختصات این نقاط درخواهیم یافت که این مختصات از الگوی دنباله اعداد فیبوناچی پیروی میکنند. این نقاط را نقاط فیبوناچی مینامند.
اعداد فیبوناچی در طبیعت
اعداد فیبوناچی و نسبت طلایی در جوانب مختلف هستی کشف شده اند. خطوط ماپیچ و اعداد فیبوناچی، حاصل نسبت های موجود بین دنباله اعداد فیبوناچی هستند.
شاخ و برگ درخت ها به صورت تصادفی در جهات مختلف رشد نمی کنند. اندازه گیری زاویه شاخه ها نشان می دهد که در الگوی رشد آن ها، نظمی شبیه دنباله فیبوناچی و نسبت طلایی وجود دارد.
پیشنهاد تی بورس : آموزش ارزدیجیتال در مشهد

در قسمت لاک حلزون از زاویه فی استفاده شده است. شاخ و برگ درخت ها به صورت تصادفی در جهات مختلف رشد نمی کنند. اندازه گیری زاویه شاخه ها نشان می دهد که در الگوی رشد آنها، نظمی شبیه دنباله فیبوناچی و نسبت طلایی وجود دارد. درختان با پیروی از این نوع الگوی رشد، قادرند درصد بیشتری از نور خورشید را جذب کنند.
نسبت طلایی (۱٫۶۱۸) در ساختار آفتابگردان نیز بکار رفته است.
دانه های آفتابگردان به شکل مارپیچ هایی روبروی هم رشد می کنند. طبق تحقیقات انجام شده نسبت قطر هر مارپیچ به مارپیچ بعدی ۱٫۶۱۸ است. حتی در ساختار شکل گوش ما هم از اعداد فیبوناچی تبعیت شده است.

نمونه هایی از نسبت طلایی در طبیعت
نسبت طلایی (۱٫۶۱۸) در آناتومی بدن انسان نیز بکار رفته است.
اگر قد خود را بر فاصله عمودی ناف تا نوک انگشتان خود تقسیم کنید، تقریبا عدد ۱٫۶۱۸ را بدست میآورید. با تقسیم طول بازوی خود از نوک انگشت بزرگ تا بالای شانه، بر فاصله نوک انگشت بزرگ تا آرنج خود نیز به این نسبت میرسید.
از آنجایی که این نسبت در بسیاری از اندازههای بدن انسان وجود دارد، از آن به نام نسبت الهی نیز یاد میشود.
علاوه بر طبیعت، از زمان باستان بسیاری از هنرمندان و معماران نیز از رابطههای ریاضی و هندسی در آثار خود استفاده میکردند. برای مثال میتوان به آثار تاریخی باقی مانده از دوران مصر باستان، یونان و رم اشاره کرد. مثلا معبد معروف پارتنون بهترین مثال از کاربرد نسبت طلایی (۱٫۶۱۸) است. نسبت عرض به طول پنجرههای مستطیل شکل معبد همگی برابر نسبت طلایی است.
در اهرام مصر نیز این نسبت بخوبی رعایت شده است. طول هر ضلع قاعده هرکدام از اهرام به ارتفاع آن، معادل نسبت طلایی میباشد.
معامله بر اساس تراز های فیبوناچی
ترازهای فیبوناچی ابزار بسیار قدرتمندی در معاملات است. معاملات میتواند فقط بر اساس این تراز ها و یا بر اساس ترکیبی از این تراز ها با روشهای دیگری مثل نمودار های شمعی، اندیکاتور ها و پترن ها انجام شود.
برای قرار دادن ترازهای فیبوناچی در چارت ابتدا باید مقادیر حداکثر و حداقل مهم چارت را بیابیم. این امر ممکن است نیازمند برگشت به عقب به مدت چند روز یا حتی چند هفته باشد. برخی از معامله گران این ترازها را روی قالب های زمانی مختلفی تا هفتگی و ماهانه قرار می دهند که این ترازها می تواند بازار را تحت تاثیر قرار دهد.
همگرائی ترازهای فیبوناچی می تواند با قرار دادن ترازهای فیبوناچی در قالب های زمانی مختلف ، پدید آید.وقتی همگرائی پدید می آید، این ترازها می توانند مهمتر قلمداد شوند. همچنین همگرائی ترازهای فیبوناچی با ترازهای حمایت و مقاومت و خطوط روند نیز مهم است.
ترازهای فیبوناچی بازگشتی
معاملات بازگشتی کم خطر تر از معامله بر اساس شکست هستند. ترازهای اصلی عبارتند از:
(۷۶٫۴%) ۷۸٫۶% ,۶۱٫۸% ,۵۰% ,۳۸٫۲%
بازار به طور معمول پس از هر حرکت قوی و قبل از ادامه حرکت، بازگشت می کند. نمی توان گفت که بازار همواره دقیقا به این تراز ها برخورد می کند. مثلا ممکن است قیمت در نقطه ای بین ۵۰ % و ۶۱٫۸ % برگردد. تراز های ۶۱٫۸ % و ۷۶٫۴ % نیز برای برگشت بسیار متداول هستند.
این تزار ها را در قالب های زمانی مختلف پیگیری کنید. بهترین راه صبر کردن تا حصول تایید برگشت روند در نزدیکترین نقطه به C قبل از ورود به معامله است. قسمت مشکل معامله بر اساس ترازهای فیبوناچی این است که دریابیم کدام یک از این تراز ها منجر به برگشت می شوند.
برای تصمیم به خرید ابتدا باید قیمت از نقطه حداقل A به نقطه حداکثر B برسد و به نقطه C بازگشت کند با تغییر جهت در نقطه C و شروع یک صعود دیگرمی توان اقدام به خرید نمود . معکوس همین حالت نیز برای اقدام به فروش صادق خواهد بود.
نقاط حداکثر یا حداقل بین روز، یک روزه، دو روزه و سه تا پنج روزه نیز دارای اهمیت خاصی هستند. الگوهای شمعی وقتی در نزدیکی تراز های فیبوناچی و سایر تراز های حمایت و مقاومت شکل بگیرند، بسیار قابل اطمینان تر هستند. نمودار های شمعی همچنین برای هشدار در پایان بازگشت نیز بسیار موثرند.
کف و سقف دوبل نیز معمولا در تراز های فیبوناچی نظیر بازگشتی %۶۱٫۸ و انبساطی %۱۲۷ تشکیل می شود.
اعداد مهم فیبوناچی
برخی از اعداد مهم دنباله اعداد فیبوناچی، برای معامله گران و تحلیل گران بازار های مالی از اهمیت خاصی برخوردارند. تحلیل گران حرفه ای در آموزش تحلیل تکنیکال معتقدند که، هنگامی که نمودار قیمت نزدیک حمایت و مقاومت ها شود، برای تعیین سطوح بازگشتی قیمت باید از ابزار اعداد فیبوناچی استفاده کرد..
اعداد مهم فیبوناچی در بازار های مالی عبارت اند از:
%23.6 – %38.2 – %50 – %61.8 – %78.6 – %100 – %161.8 – %261.8 – %423.6
اکثر اعداد مهم فیبوناچی خاصیت حمایی و مقاومتی برای نمودار قیمتی دارند. همچنین در مواقعی از آنها به عنوان سطوحی که قیمت سهم یا ارز مربوطه می تواند به آن ها برسند، استفاده می شود.
تعدادی از صاحب نظران در تحلیل تکنیکال معتقدند به علت تنوع زیاد سطوح اعداد فیبوناچی، ممکن است معامله گران در تعیین معتبرین سطح در معاملات خود دچار اشتباهات و اختلاف نظر شوند.
اعداد فیبوناچی اصلاحی
فیبوناچی اصلاحی یا Fibonacci Retracement در تعیین سطوح حمایتی و مقاومتی کاربرد دارد. فیبوناچی اصلاحی فرمولی برای محاسبه و تحلیل ندارد. تنها براساس اعداد موجود در بازه قیمتی که توسط دو نقطه برای آن مشخص میشود برخی از درصد های مهم را تعیین میکند.
مهم ترین سطوح و اعداد فیبوناچی اصلاحی که با آنها سروکار داریم، سطوح 23.6%، 38.2%، 50%، 61.8% و 78.6% هستند.
در ادامه نمونهای از استفاده از ابزار فیبوناچی اصلاحی در تریدینگ ویو را بررسی میکنیم.
بیشتر بخوانید: بهترین استراتژی با اعداد فیبوناچی فارکس
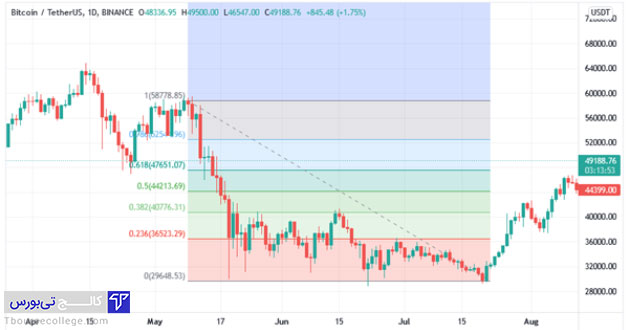
چارت فوق نمودار قیمتی BTC/USDT است. با استفاده از ابزار Fib Retracement، نقطه ابتدایی را در سطح قیمتی 58800 و نقطه دوم را در سطح 29600 رسم کردیم.
همان طور که مشاهده میکنید سطوح فیبوناچی اصلاحی به صورت خودکار در سطوح قیمتی مختلف، بین دو نقطهای که مشخص کردیم تشکیل شدند.
به عنوان مثال سطح 0.236 همان سطح 23.6% است که سطح قیمتی 36523 را نشان میدهد. به صور مشابه سطح 0.382 همان سطح 38.2% است که در اینجا به عنوان یک سطح مقاوتی در قیمت 40776 ایجاد شده و از افزایش قیمت جلوگیری کرده است.
نکته مهمی که در رابطه با سطوح و اعداد فیبوناچی اصلاحی باید مد نظر داشته باشید. این است که اعتبار آنها همیشه زیاد نیست. به عبارتی هنگام نزدیک شدن قیمت به این سطوح سعی کنید رفتار قیمت را از لحاظ پرایس اکشن نیز بررسی کنید و با توجه به واقعیت حاکم در بازار، منطقی ترین استفاده را از اعداد و سطوح فیبوناچی اصلاحی ببرید.
کاربرد اعداد فیبوناچی
اعداد فیبوناچی دنبالهای از اعداد ریاضی هستند که در شکل معروف 1، 1، 2، 3، 5، 8، 13، 21 و غیره تشکیل میشوند. این دنباله در زمینههای مختلفی مانند ریاضیات، بازارهای مالی، طبیعت، موسیقی و غیره کاربردهای بسیاری دارد.
در مورد کاربردهای آن در بازارهای مالی، نسبتهای فیبوناچی میتواند به عنوان سطوح مهمی برای تحلیل و پیشبینی قیمت استفاده شود. برای مثال، نسبتهایی مانند 0.236، 0.382، 0.618، 1.618، و غیره براساس دنباله فیبوناچی ایجاد میشوند و میتوانند نقاط قوی تغییر جهت در قیمت را نشان دهند.
علاوه بر این، در طبیعت نیز استفادههایی از اعداد فیبوناچی وجود دارد. برخی از الگوها و ساختارهای موجود در طبیعت مانند شکل های گلها، قشر های صدفها و الگوهای روی خالصها مرتبط با اعداد فیبوناچی هستند.
اعداد فیبوناچی نیز در ریاضیات، هندسه، موسیقی و دیگر زمینههای دیگر نیز کاربردهای متعددی دارند. این اعداد در ایجاد الگوها، استفاده از نسبتهای هندسی و تعیین ساختارهای مرتبط بسیار مفید و کمککنندهاند.
مقالاتی که پیشنهاد میکنیم برای آموزش رایگان سرمایه گذاری مطالعه کنید
آیا می دانید کدام بازار مالی برای شما سودآورتر است؟
جهت دستیابی به جواب این سوال، در کارگاههای رایگان زیر شرکت کنید.



دیدگاهتان را بنویسید